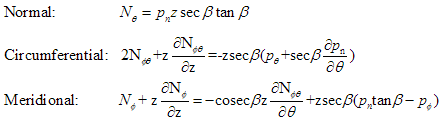Introduction to Shell Theory
Preamble
A brief introduction to the most relevant aspects of shell theory that we have covered so far will be given here.
The stresses and displacements that occur in silo shells can be derived from both bending and membrane theories (Rotter 2001). The former is a full theory of shell bending applicable for all conditions and geometries of silo giving quite precise, though laborious results, taking both bending and membrane phenomena into account (Rotter, 1987a). The latter ignores bending moments and bending stresses, as well as the associated large elastic displacements, and deals only with membrane stresses caused by in-plane forces (not bending moments), and therefore allows for a much quicker and more simplified analysis on most parts of the silo. Both theories are equally applicable for both the barrel and the hopper.
Under both axial and distributed normal loading, membrane theory provides a sufficiently accurate analysis for both axisymmetric and non-symmetric (and eccentric) loading cases for smaller-scale silos (Rotter, 2001). This is provided the analysis is carried out on a point distant from any discontinuities such as material joints, section boundaries, changes of cross-section or plate thickness, locations of applied loads, ring stiffeners and, most importantly, the transition ring between silo barrels and hoppers. These discontinuities are the regions of highest local bending (Rotter, 1987b) in which bending stresses can no longer be ignored, and a full bending analysis should to be used.
However, the most crucial part of the silo is the transition between the silo barrel and the hopper. This highly-stressed area is often strengthened by the presence of a ringbeam, which limits excessive deformations and bending due to material plasticity (Rotter, 1985). This elastic-plastic behaviour (as opposed to purely elastic behaviour for bending) actually allows one to apply membrane theory to regions of the hopper much closer to the silo-hopper transition thus making the following membrane equations valid across most of the hopper height.
Initially, we shall limit ourselves to membrane theory. As time goes on and we gain more experience in the subject area we will begin to explore bending theory in more detail. Consequently, the next section will explore some of the derivations in membrane theory that we have done so far.
Membrane Theory Equations top Δ
Since the stress resultants originating from bending stresses and radial shear are ignored, the only stresses present are those caused by in-plane forces as a result of applied loadings. Such loadings may include internal normal pressures, vertical downward friction and discrete point loads due to column supports.
The above simplification allows the derivation of three static equilibrium differential equations for both the silo barrel and hopper (cylindrical and conical shapes respectively), one for each dimension, which can then be used to calculate the membrane stresses resultants. Since membrane stresses are constant throughout the thickness of the shell, they are obtained very simply by dividing the resultants by the thickness:
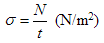
Cylindrical Sections top Δ
Figure 9 shows an infinitesimally small cylindrical element showing these stress resultants (blue) as well as the applied loadings (red).
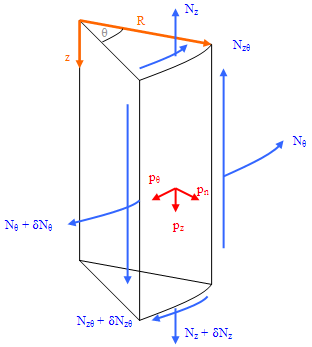
Fig. 9 - Stress resultants, cylindrical section
Nz, Nθ – membrane stress resultants in the axial and circumferential directions (N/m)
Nzθ – shear stress resultant (N/m)
pn, pθ, pz – distributed surface loadings in the normal, circumferential and axial directions (N/m2)
R – radius of the silo barrel / cylinder (m)
θ – angle of spread
The three basic equilibrium equations are thus, and their derivation (derived by us, of which we are very proud) is available in pdf format:
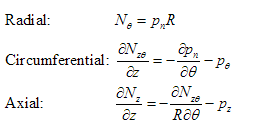
These are valid for both axisymmetric and non-symmetric conditions. The former case allows their further simplification (no variation around the circumference, hence δθ vanish and pθ becomes zero) , whilst the latter case necessitates their further complication with the help of Fourier series which attempts to model the non-symmetrical loading pattern as it varies with the angle θ around the circumference. The loadings are approximated by Fourier ‘coefficients’ which are incorporated into the above equations. The Fourier series is mathematically given as (James, 2001):
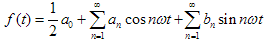
where every value of n represents a ‘harmonic’.
The following Java applet gives the reader a taste of how the Fourier series does this. Just play around with the load and angle of spread (the centre of this spread will always be at maximum load), but most importantly with the value of the Fourier harmonic, to see how the load is approximated. You need a high harmonic value to get a shape resembling the supposed load pattern. This implies very long series which, if to sum by hand and not by computer, would be a very tedious task. The three load patterns represented are rectangular, linear patch and smooth-edged patch loads respectively, with formulae from Rotter, 1987a, Appendix I.
Conical Sections top Δ
The equilibrium equations may also be derived for an infinitesimally small conical shell element (analogous to the hopper), as shown in Figure 10 below, in the same way as for the cylindrical element.
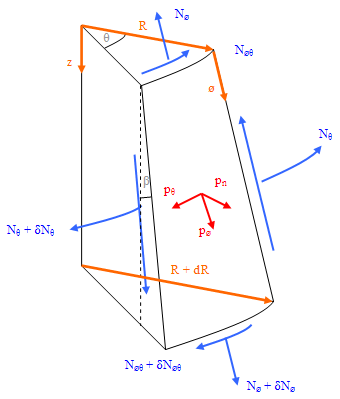
Fig. 10 - stress resultants, conical section
N∅, Nθ – membrane stress resultants in the meridional and circumferential directions (N/m)
N∅θ – shear stress resultant (N/m)
pn, pθ, p∅ – distributed surface loadings in the normal, circumferential and meridional directions (N/m2)
R – radius of the silo barrel / cylinder (m)
θ – angle of spread
The three basic equilibrium equations are thus, whose derivations (also derived by us, of which we are even more proud, as they were more difficult) are also available in pdf format: